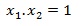MATERI LENGKAP: Persamaan Kuadrat
Halo semua sahabat ID-KU .Pada kesempatan ini, Ilmuku duniaku akan memposting materi matematika SMA tentang “Materi Lengkap Persamaan Kuadrat”. Adapan submateri pada materi lengkap persamaan kuadrat ini adalah sebagai berikut:1. Pengertian Persamaan Kuadrat
2. Cara Penyelesaian Persamaan Kuadrat
3. Menentukan Jenis Akar-akar Persamaan Kuadrat
4. Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat
5. Sifat-sifat Akar Persamaan Kuadrat
6. Menyusun Persamaan Kuadrat
Baca Juga: Barisan dan Deret, Trik Matematika, Rumus Praktis
1. Pengertian Persamaan Kuadrat
Persamaan kuadrat adalah suatu persamaan yang pangkat tertinggi dari variabelnya adalah 2.
Bentuk umum persamaan kuadrat:
ax2 + bx + c = 0, a≠0 dan a,b,c elemen R
Dengan: x adalah variabel dari persamaan kuadrat a adalah koefisien x2b adalah koefisien xc adalah konstanta
Baca juga : Contoh Soal Persamaan Kuadrat2. Cara Penyelesaian Persamaan Kuadrat
Ada 3 cara untuk menyelesaikan soal-soal yang berbentuk persamaan kuadrat yakni:
a. Memfaktorkan
ax2 + bx + c = 0, a≠0 dapat diuraikan menjadi: (x – x1) (x – x2) = 0
b. Menggunakan Rumus Kuadrat (Rumus abc)
Rumus untuk menentukan akar-akar persamaan kuadrat ax2 + bx + c = 0, a≠0 adalah:
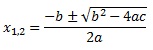
c. Melengkapkan Kuadrat Sempurna
Cara menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna adalah dengan mengubah persamaan kuadrat menjadi bentuk kuadrat sempurna. Bentuk umum persamaan kuadrat berbentuk kuadrat sempurna adalah
(x+p)2 = q, dengan q > 0
Baca Selengkapnya: Contoh Soal Cara Menentukan Akar Persamaan Kuadrat
3. Menentukan Jenis Akar-akar Persamaan KuadratJenis akar-akar persamaan kuadrat ax2 + bx + c = 0 dapat ditentukan oleh nilai diskriminan D = b2 – 4ac a. Kedua akar nyata dan berlainan (x1 ≠ x2) <=> D > 0b. Kedua akar nyata dan sama (x1 = x2) <=> D = 0c. Kedua akar tidak nyata (imaginer) <=> D < 0d. D = k2, dengan k2= bilangan kuadrat sempurna kedua akar rasional4. Jumlah dan Hasil Kali Akar-akar Persamaan KuadratUntuk menghitung jumlah dan hasil kali akar-akar persamaan kuadrat ax2 + bx + c = 0, dengan a≠0 dapat dicari tanpa terlebih dahulu mencari akar-akarnya.
Dari rumus:

dapat diperoleh:
x1 + x2 =-b/a dan x1.x2 = c/a
Rumus-rumus lain yang dapat digunakan adalah
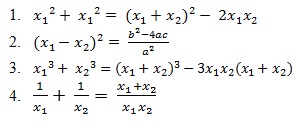
5. Sifat-Sifat Akar Persamaan Kuadrat
Jika x1 dan x2 adalah akar-akar persamaan kuadrat ax2 + bx + c = 0, a≠0 maka berlaku sifat-sifat berikut ini:
a. Syarat mempunyai dua akar positif

b. Syarat mempunyai dua akar negatif
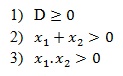
c. Syarat mempunyai dua akar berlainan tanda
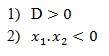
d. Syarat mempunyai dua akar berlawanan
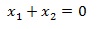
e. Syarat mempunyai dua akar berkebalikan